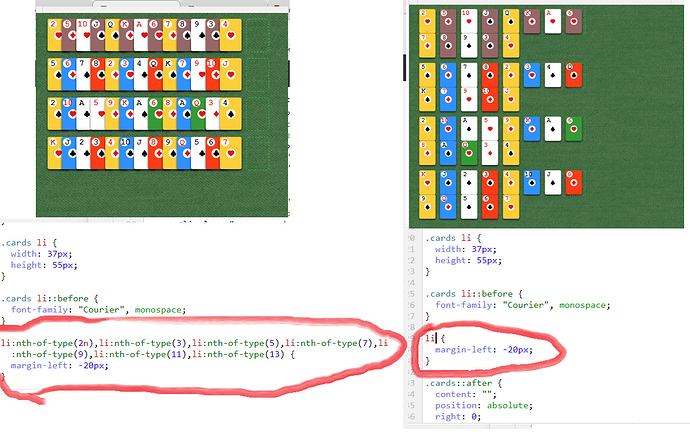
Здравствуйте, неужели просто li и li:nth-of-type(выбранные по очереди все элементы LI из списка)
не одно и то же:
почему код себя так по-разному ведет?
Прилагаю на всякий случай полный код и скриншот поведения кода Испытание: вторая раскладка
html,
body {
margin: 0;
padding: 0;
font-family: “Arial”, sans-serif;
}
body {
min-width: 550px;
min-height: 250px;
padding: 10px;
}
.cards {
position: relative;
width: 380px;
text-align: left;
}
.cards li {
width: 37px;
height: 55px;
}
.cards li::before {
font-family: “Courier”, monospace;
}
li:nth-of-type(2n),li:nth-of-type(3),li:nth-of-type(5),li:nth-of-type(7),li:nth-of-type(9),li:nth-of-type(11),li:nth-of-type(13) {
margin-left: -20px;
}
.cards::after {
content: “”;
position: absolute;
right: 0;
top: 0;
display: block;
width: 37px;
height: 55px;
border: 1px dashed #33bb33;
border-radius: 5px;
}
ul li:nth-child(4n+1) {
background-color: #ffcc33;
}
ul:not(:first-of-type) li:nth-of-type(4n+2) {
background-color: #0099ff;
}
ul:nth-of-type(even) li:nth-child(4n) {
background-color: #ff3300;
}
ul:nth-of-type(3) li:nth-last-of-type(3),
ul:nth-of-type(3) li:nth-last-of-type(6)
{
background-color: #339933;
}
ul:first-of-type li:nth-child(2n){
background-color: #996666;
}